Speciation from inbreeding #
Disclaimer: I am not a biologist. I'm interested in this topic but I haven't studied it that much. These are my random thoughts on how a species can form:
It seems to me that we only “need” new species when things are going badly. In these stressful situations, the population of an existing species will decline. A small population is more likely to lead to inbreeding/incest. What happens with inbreeding? We get increased mutations. The history of royalty in Europe has some examples (hemophilia, six fingered folk, etc.). It's exactly when things are going badly with a species that a new species has a chance, and I think it's no coincidence that mutation rates are higher then.
More specifically, I think susceptibility to mutation is an evolved characteristic. Species that “fixed” the problem with genetic errors would not evolve, and would eventually be wiped out. Only the species that had mutations would survive. Secondly, I think the mutation rate varies, and it responds to stress and inbreeding, not by accident, but because a variable mutation rate evolved as well. When a population no longer fits well into the environment, it needs to increase the mutation rate so that it can turn itself into a new species.
A consequence of this line of thinking is that when populations are large, we should rarely see new species form. We shouldn't see many new species forming until the environment changes drastically.
I also think in extreme cases, a very small population might lead to asexual reproduction with a high mutation rate. Species that allowed for asexual reproduction in rare cases are more likely to survive.
If small populations lead to new species, what would we observe?
- If there are several populations of a species, and one of them mutates into a new species, we will see a new species and call it a “branch” on the tree of life.
- If on the other hand the small population is the only surviving instance of a species, then as it turns into a new species, the old species will be wiped out. There may be no record of it. In the tree of life, we would only see two distinct species if the creatures are physically different and if both populations left fossils.
I think most new species are of the latter form, and never show up in the fossil record. How could I call this a new species then? If we had a time machine and brought a creature of the first form forwards in time, and it tried to breed with a creature of the second form, we'd be able to decide whether the old and new creatures are genetically compatible. If they are, I'd say they are the same species. But in a lot of cases, they won't be able to interbreed, and we have a new species. We can't really test this without a time machine.
To summarize: I think that variable-rate mutation is an evolved behavior that shows itself when populations are small and stressed, and that there have been a lot more species than the ones we see in the fossil record.
Labels: future
Emacs: move autosave and backup files elsewhere #
One thing that really bugs me about Emacs is the way it clutters up my directories with backup files (filenames ending in ~) and autosave files (filenames starting with #). Fortunately there's an easy way to move them elsewhere. Unfortunately the technique isn't consistent across Emacs versions. In GNU Emacs 21, you can set backup-directory-alist and auto-save-file-name-transforms. In XEmacs 21, you can set bkup-backup-directory-info and auto-save-directory. Here's what I do in GNU Emacs:
(defvar user-temporary-file-directory (concat temporary-file-directory user-login-name "/")) (make-directory user-temporary-file-directory t) (setq backup-by-copying t) (setq backup-directory-alist `(("." . ,user-temporary-file-directory) (,tramp-file-name-regexp nil))) (setq auto-save-list-file-prefix (concat user-temporary-file-directory ".auto-saves-")) (setq auto-save-file-name-transforms `((".*" ,user-temporary-file-directory t)))
Here's what I do in XEmacs:
(require 'auto-save) (require 'backup-dir) (defvar user-temporary-file-directory (concat (temp-directory) "/" (user-login-name))) (make-directory user-temporary-file-directory t) (setq backup-by-copying t) (setq auto-save-directory user-temporary-file-directory) (setq auto-save-list-file-prefix (concat user-temporary-file-directory ".auto-saves-")) (setq bkup-backup-directory-info `((t ,user-temporary-file-directory full-path)))
I'm much happier with Emacs temporary files being kept out of my way.
Labels: emacs
Emacs: don't kill unsaved buffers #
Long ago, I added a key to Emacs to quickly close a buffer. I used to use Alt+F3, because that's what I used with Turbo Pascal. These days I use Cmd+W to match the Macintosh key for closing windows. The trouble is that when it's easy to close buffers, I do it often, and I occasionally close a buffer I shouldn't have closed. The solution is to make Emacs ask me for confirmation if the buffer hasn't been saved.
In both GNU Emacs and XEmacs, the answer is in a variable named kill-buffer-query-functions:
kill-buffer-query-functions is a variable defined in `C source code'. Documentation: List of functions called with no args to query before killing a buffer. The buffer being killed will be current while the functions are running. If any of them returns nil, the buffer is not killed.
Emacs will call each function listed in kill-buffer-query-functions before killing a buffer. If any of these functions returns nil, Emacs will not kill the buffer. So I defined a function that would ask for confirmation if the buffer hadn't been saved:
(defun ask-before-killing-buffer ()
(cond
((and buffer-file-name (buffer-modified-p))
(y-or-n-p (format "Buffer %s modified; kill anyway? "
(buffer-name))))
(t t)))
(add-to-list 'kill-buffer-query-functions
'ask-before-killing-buffer)
I then extended this function to not kill the *scratch* buffer, and ask for confirmation before killing shell buffers that have an active process:
(defun ask-before-killing-buffer () (let ((buffer (current-buffer))) (cond ((equal (buffer-name) "*scratch*") ;; Never kill *scratch* nil) ((and buffer-file-name (buffer-modified-p)) ;; If there's a file associated with the buffer, ;; make sure it's saved (y-or-n-p (format "Buffer %s modified; kill anyway? " (buffer-name)))) ((get-buffer-process buffer) ;; If there's a process associated with the buffer, ;; make sure it's dead (y-or-n-p (format "Process %s active; kill anyway? " (process-name (get-buffer-process buffer))))) (t t)))) (add-to-list 'kill-buffer-query-functions 'ask-before-killing-buffer)
The ironic thing is that since I wrote that function, I haven't accidentally tried to close a buffer...
Labels: emacs
Paradox of Choice #
I've been reading The Paradox of Choice, a book about more choices not always being better. There's also a one hour talk by the author. It made me think about how we might model choices, either for understanding our own behavior or for writing simulation games. The author of the book argues that at an abstract level people understand the benefit of additional choices but ignore their costs, whereas in practice people are affected by those costs, albeit not always in a rational way.
To model the benefit of choice, I'm going to say that if there are N-1 choices, and you are presented with 1 additional choice, your benefit has increased. By how much? It's only a benefit if the new choice was better. Since there are now N choices, let's say the probability the new one is better is 1/N. If it is better, by how much is it better? I think you can build an expectation function based on the distribution (for example, a gaussian distribution), but I'm going to be simplistic and say the benefit is constant. The new item is always 1 unit of value better than the old one. In practice I think the benefit decreases as the number of choices goes up, so I'm being generous here. So the added benefit of the Nth choice is the probability it's better multiplied by the amount it's better: 1/N * 1. To determine the total benefit, we have to sum from choice 1 to choice N, and we end up with something approximately equal to the logarithm: ln(N).
To model the cost of choice, I'm going to say that you have to make the comparison between the new item and the old items, even if the new item isn't better. You might compare to each of the old items, giving a cost of N, or maybe you only compare to the best of the previous items, giving a cost of 1. I'm going to be generous here and say the added cost is just 1. The total cost then is 1 for each new item, or a total of N.
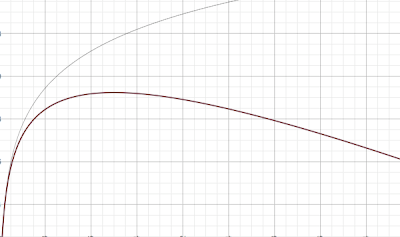
So now we have a model in which both the benefits and costs go up as the number of choices increases. Each additional choice brings smaller and smaller benefits but larger and larger costs. Here's a plot of what this might look like:
Initially having choices greatly adds to your well-being. However, the rising costs eventually overtake the diminishing benefits, and the total value of having choices goes down. This seems to be the main message of the book: that additional choices do not always make us better off.
When I defined the model, I decided to be generous. The incremental benefit is 1 in my model, but it's probably decreasing as the number of choices goes up. This means the total benefit is lower than in my model. The incremental cost is 1 in my model, but it's probably increasing as the number of choices goes up, because people at some level will compare to all the alternatives, not just one. This means the total cost is higher than in my model. So the graph above is optimistic; in reality it probably drops even faster.
Note that the graph has no scale. That's because I think the costs and benefits will depend a great deal on the situation. When buying toothpaste, the benefit of more choices is pretty limited. But when choosing a job or spouse, it makes a much larger impact on your life. The main point is that additional choices will eventually not be worth the cost of evaluating them, so at some point you should just make your decision and not worry about it anymore.
Labels: economics